近日，葡京集团娱乐网址394李翔宇教授课题组在非规则构型压头接触问题的研究方面取得进展，相关成果以“Accurate prediction of contact stiffnesses of irregular interfaces”为题发表在国际应用力学和机械科学领域权威期刊《International Journal of Mechanical Sciences》。西南交通大学力学与航空航天学院博士研究生王永彬为论文第一作者，李翔宇教授为通讯作者，合作作者包括葡京集团娱乐网址394储节磊副教授，袁江宏副教授、康国政教授和浙江大学陈伟球教授（图1）。
论文链接：https://doi.org/10.1016/j.ijmecsci.2025.110969
图1. 论文首页
接触式转印技术对新一代电子产品的制造至关重要，但接触过载不可避免地会导致转印失效，从而影响电子产品的成品率。避免接触过载最有效的方法之一是在目标物体的转印过程中，准确获得与目标物接触有关的接触力与变形之间的关系，以确定与不同接触目标相关的接触力的极限值。接触刚度作为确定接触力和变形之间关系的基本物理参数，它的准确预测是获得接触力极限值的有效途径。然而，为了实现特定的功能，新型电子器件的几何形状通常具有复杂的非规则构型。这使得传统的理论或数值工具在确定相应界面的接触刚度时存在挑战，因为接触界面上多个非规则压头之间存在复杂的弹性相互作用。
精确表征非规则构型压头之间的弹性相互作用是准确确定具有非规则构型压头接触界面接触刚度的关键。尽管可以采用层级填充策略将非规则接触界面离散为层级结构多压头接触界面，从而将各种复杂的非规则边界将转换为简单的圆边界，并借助多压头接触界面接触刚度的理论模型[1]准确表征层级圆压头之间的弹性相互作用，进而等效确定非规则接触界面的接触刚度，但这一离散化填充和相应的预测过程需要耗费大量的时间。
|
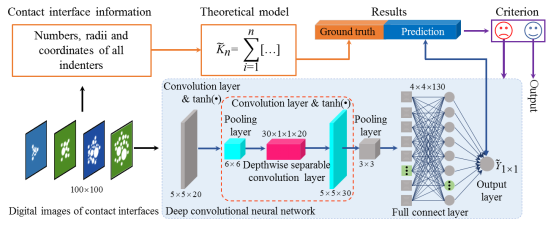
图2. 深度学习模型（DCNN）的结构和工作流程。新引入的三个层标记在红色虚框中；灰色层为经典的卷积神经网络（CNN）结构，深度可分离卷积层用红色六面体表示。 |
此外，接触界面的接触刚度和真实接触面积的平方根成正比[2]。为了提高预测的准确性，接触界面上圆压头的填充率应理论的趋近于1。在层级填充策略中，虽能通过减小最小填充压头的半径提高层级填充压头的填充率，但考虑到实验中制造精度的限制和数值计算中有限步长的要求，获得零半径填充压头并不现实。因此，接近1的填充率在现实中难以实现。
|
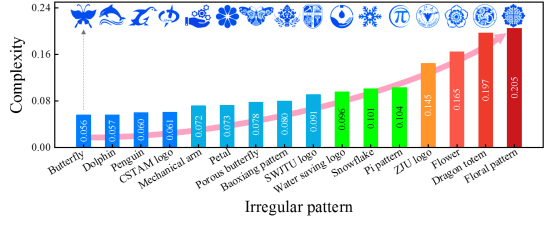
图3. 非规则图案界面复杂度的评估结果。每个色条的值对应所指示样本图案的复杂度。 |
李翔宇教授课题组针对该问题，构建了深度学习模型（图2），从图案化的角度预测具有复杂非规则构型接触界面的接触刚度。在网络架构方面，设计了具有特征融合能力的深度可分离卷积层，来表征非规则压头间复杂的弹性相互作用；在特征评价方面，引入图案的复杂度指标，从样本构型的复杂程度来量化和确保样本的几何多样性；在模型性能评估方面，通过系统的压痕实验检验深度学习模型的预测精度和泛化能力。
|
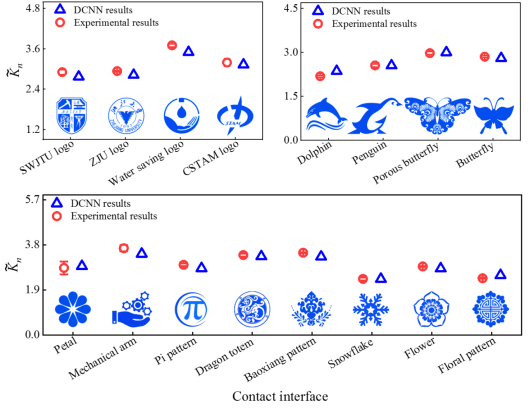
图4. 由深度学习（DCNN）模型预测和实验测量的具有非规则构型接触界面的归一化接触刚度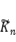 。每个样本五次实验的平均值和标准差分别用红色的空心圆和误差条标记。 |
建立的深度学习模型能表征接触界面上压头之间的弹性相互作用，并表现出卓越的预测能力与鲁棒的泛化能力。即使对于那些几何构型高度复杂的不规则样本（图3），当前深度学习模型的预测结果与实验数据高度吻合（图4）。此外，本研究引入的图案复杂度概念，消除了深度学习中仅依赖人直观感知评估样本特征多样性的非理性评估方式。这是深度学习中各类预测目标特征多样性评估的实质性进展。
当前的深度学习模型具备超快的预测能力，单个样本的预测可在0.2秒内完成。当前的研究极大提升了不规则接触界面接触刚度的预测效率。基于深度学习模型给出的接触刚度，可准确获得定制硅片的极限荷载（图5），从而避免了转印过程中因接触过载导致的硅片失效。当前的研究对新一代电子器件制造的关键工艺－巨量转移技术的安全性与可靠性具有重要意义。
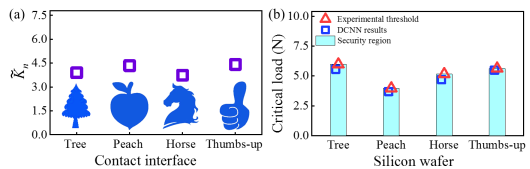
图5. 通过硅片的拾取实验验证当前的深度学习模型（DCNN）。 (a)当前模型预测的具有定制化“树状”、“桃子”、“马头”和“点赞”图案接触界面的归一化接触刚度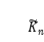
。(b)当前深度学习模型确定的具有定制化“树状”、“桃子”、“马头”和“点赞”图案硅片的临界载荷。
该研究受到了国家自然科学基金重大项目子课题(Nos.: 12192210, 12192211)、国家自然科学基金面上项目(Nos.: 12072297, 62276218)的支持。
参考文献
[1] Wang Y, Zhao J, He Y, Yang M, Chu J, Yuan J. Li X, Chen W. Contact stiffness of the multi-indenter contact interface[J]. Journal of the Mechanics and Physics of Solids, 2024, 188: 105659.
[2] Kendall K, Tabor D. An utrasonic study of the area of contact between stationary and sliding surfaces[J]. Proceedings of the Royal Society A, 1971, 323: 321-340.
